Using a Stryd Sensor to Do Pace Based Workouts
Sep 19, 2020
20 mins read

Preamble
This article is nor a presentation of the Stryd sensor, nor a description of its use. It is aimed at those who know the concept of running power and who own a Stryd sensor.
It describes the inner algorithm of the Garmin watch app Flat Pace and a full-scale test. This is not a tutorial, nor a documentation of this data field.
Why prefer speed?
It may seem absurd, to equip yourself with a power meter costing 200$ and use it only to measure the speed. Of course, it is true that the precision of the pace and the distance that this sensor gives are impressive1. And we can really pretend that it reduce the GPS only to the navigation and we can completely ignore it for the training analysis.
But, the main reason for choosing pace over power comes from the nature of the unit of measurement. It is difficult to interpret a value in watt. It may even be that running at 300W is slower for one athlete than running at 250W for an other because the energy to be supplied to maintain speed largely depends on the weight of the athlete and his racing style.
The power is directly related to the effort provided and it does not does not rely on the terrain and conditions weather. But, the interpretation of his value requires some experience. Over time, the runner is able to create a correspondence between the pace and the measured power.
However, this connection is not always obvious and it may vary cover the time. In my case, I experienced it after having lost 2-3kg, the power has been recalculated with the effect that the correspondence I had in mind was no longer applicable.
That said, one could retort, that it would be wise to work only using the power zones which are recomputed automatically by Stryd. But, ignoring the pace is not really so easy because:
- Many training programs are based on pace.
- Coaches often rely solely on frequencies heart rates and speeds. They don’t integrate power in their analysis.
- It is impossible to compare the powers between the runners so values differ between individuals.
In short, we can turn things in all directions, the power is great for replacing speed during training. But without knowing the correspondence between the two metrics, it does not replace its measure, it completes it.
In this situation, we are in front of 3 different measurements to analyze (the heart rate, speed and power). This complicate the analysis of runs at the risk of using a labyrinthine system for interpretation. Look at what some platforms provide: power, pace and heart rate zones, histograms, curve of the evolution over the distance, maximum in the race… In short, at the end, the result is accumulating graphics and tables and losing the overview.
One solution is to replace power with speed equivalent on an athletics track. In this case there is a linear correspondence between speed and power. Basically, if running at 200w is corresponding to 10km/h and 300w to 20km/h, then 250w is corresponding to 15km/h. It is also remarkable that performance tests for athletes are implicitly using this characteristic. To determine lactic thresholds, for example, a typical test can be performed on a treadmill whose imposed speed permits to control the power supplied by the muscles.
The equivalent pace on an athletic track simplifies many things. In the case of a training plan based on the paces, it can directly used do do hill workouts because the computed pace ignore the effect of the ascent (whereas the instantaneous measured value is often difficult to interpret). But, even more interesting, during a race, it can be used to follow a target pace which is decorrelated from field irregularities.
Stryd proposes to determine the relationship between power and speed2 through a protocol. This requires performing intervals on the track at different speeds and then to measure their associated powers. Then it is only necessary to determine the correspondence through a simple sheet which shows the pace associated for each power value. It is easy but it is of course necessary to repeat this run from time to time to maintain the table up to date.
Estimate the VO2max with a protocol (like a Conconi test which gives the VMA and permits then to compute the VO2max) is one standard way, but an other consists to use algorithms that evaluate it continuously by analyzing running history (this is what most of the watches are providing). In the same way, we can use an algorithm which calculates the pace/power correspondence in real time.
Let see how this works with “Flat Pace” for Garmin watches.
A bit algorithmic
In general, few companies explain the principle of their algorithms works under cover of protection of their intellectual property. For my part, I believe that understanding the principle allows a better usage.
Any algorithm has a domain of application. Knowing it, allows to limit its usage to the environment designed for and so to avoid fancy results.
The explanation that I will try to give will only expose the basics to permits an optimal usage.
Speed and power measurement
Before an analysis can be made, it is necessary to measure with precision. This might sound trivial, but it’s not really:
- The power is directly supplied by the Stryd sensor in using the ANT+ interface. This helps to support Garmin watches that do not officially offer racing power (like the Forerunner 245 or Vivoactive 3).
- The speed does not come directly from the sensor but from the watch. This poses a small problem, as it can be determined by the GPS and not the Stryd sensor.
The speed measured by the GPS is initially not as precise and it suffers from a higher latency. It is not determined after 2-3 seconds but often after twenty and, in addition, it is not instantaneous but averaged over this period. It is therefore better to change the source of speed and distance in watches and set it to the Stryd foot pod. (at least for the watches which support it like the Forerunner or Fenix)
I use a technique to handle the speed provided from the GPS which consists to take every 25s the most stable pair of power and speed during 5s. This has the advantage to make it compatible the very popular 30/30 training intervals. It ensure that the measurements do not correspond to the unstable phase of acceleration or deceleration.
Calculation of the relationship between power and speed
In a very simplistic approach, the relationship between power and speed is purely linear:
$$ Speed = a \times Power $$
However, this is only true if we just consider the power used for the horizontal displacement. There is also a significant part lost laterally or vertically. Stryd talks about Form Power. So, to this formula we add a constant loss parameter by making it affine:
$$ Speed = a \times Power + b $$
As the relation is not 100% affine and a small curvature may exist, we frame this formula by a convex function (here a power greather to one) and a concave function (the square root):
$$ Speed = a \times Power + b + c \times Power \sqrt{Power} + d \times \sqrt{Power} $$
The algorithm tries to determine these four parameters and then uses this formula to deduce the speed associated with the power.
Case of walking
It should be noted that when walking, the power is quite different as when running. The Form Power and also the overall power are decreasing and are no more following the same physical laws. Therefore, the formula for calculating speed cannot be applied to walking. Also, it is necessary to suspend the learning process of the algorithm when walking.
For this reason, a minimum running pace parameter (9:00 min/km) is use a threshold to filter the walking phases. It can be changed by editing the settings in ConnectIQ.
Slope detection
To work, the algorithm must only learn measurements when racing on flat ground. We could use the ascent or descent provided by the watch but the accuracy of the barometric sensors is too poor for recognizing correctly slopes and, in any way, the sensor is not present on all watches.
For this reason, we exploit the hypothesis that if we run faster on a flat road, the power increases. This may seem trivial, but when climbing, we find ourselves in the opposite case: the power increases while the real speed decreases.
In a simplistic way, we estimate that the speed in this case must follow a simple affine growing curve (with e> 0): $$ Speed = e \times Power + f $$
We then consider that the measured speed is vitiated by an error by the formula:
$$ Error = \lvert Speed - (e \times Power + f) \rvert $$
The two parameters e and f are then learned during the race. And, the calculated error is used to give a greater or lesser weight to the measurement: the lower it is, the higher will be its impact on the formula for calculating the pace on the track.
Parameter estimation
The parameters are estimated using the least mean squares algorithm which optimally minimizes the variance between the theoretical curve and the measurements.
As there are 6 parameters in all to estimate, at least 6 measurements are required. So, during a first use, you have to wait about 3 minutes before being able to have a first estimate of the speed on the track. Then, every 25 seconds, the algorithm corrects itself to stick as closely as possible to all of the measured values.
It should be noted that at the end of a session, the parameters are saved and that the history consider the last six hours of running per default (configurable by GarminIQ).
Practical implications
In general, it is advisable to do a calibration to avoid learning inconsistent values from the start.
It is best to proceed as follows:
- make your first race on a flat and windless road.
- as only the learned configurations can be calculated correctly, it is necessary to try to cover the whole range of speed, from slowest to fast.
- you have to run blocks at constant speed for 30s to obtain the most precise measurements possible.
- after 5 minutes of use, you can run quite normally and the displayed pace is refined during the further runs.
Real-life test
Theory is one thing, but let see what happens in a real-life test. For that, the first thing to do is a calibration run in an ideal environment (no wind, no height differences). Then, we move on to terrain with steep climbs and descents or with strong wind conditions to test the relevance of the computation.
Calibration run
Algorithm learning phase.
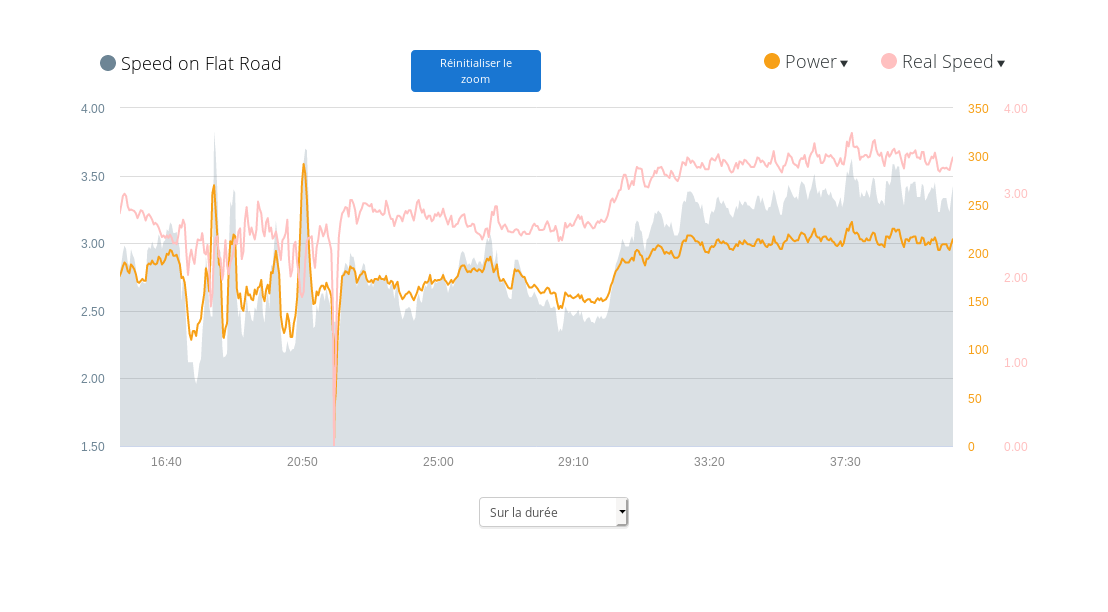
Here are the first 10 minutes of run on a road with a fresh installation of the data field .

During the first minutes (part A), no data is available, it is then impossible to estimate the pace on the track. Garmin Connect displays a flat line for its speed (gray color) which in this case simply means that no value is not available. It takes two minutes for getting a first result of the calculation. And we see that the values produced are still very unstable: I was running at a constant speed of 2.7 m/s, the estimated speed on a flat track oscillates from 2 m/s to 4.5 m/s. It is necessary to wait 5 minutes of running to get consistent and stable values.
During the first 10 minutes, the pace was constant and we see that the pace on flat track ends up being almost identical to that measured. However, around 8 minutes (marker B), there was a slight climb of about ten meters where the power increased substantially to an unknown value for the algorithm (200w). The calculated value is therefore still inconsistent: power increases but track speed decreases very noticeably to go from 2.8 m/s to 2 m/s, an aberration.
To solve the problem, I decide to run 30 seconds over 200w (marker C). We see that in the first seconds, the algorithm messes up again and is unable to calculate a speed but after 20s, learning the new correlation speed/power, it corrects itself and then produces a substantially equivalent speed (4.0 m/s against 3.7 m/s).
Analysis of calculations after the calibration phase
After 15 minutes, I forked onto a wooded trail. Winding roads, very short climbs from 10m to 15m, steep descents, tree trunk to span… The power and instantaneous speed are no longer reliable and but nothing better for to test the resistance to disturbances on computation…
Going out of the forest, a soft downhill at constant speed, the estimated speed on the flat decreases and follow to the power. It’s consistent: downhill running requires less effort as on a flat road, it’s a bit like running slower on a track.
Then, a soft uphill and the opposite effect is observed: the estimated speed increases compared to the actual speed which is also coherent.
Finally, I did a stage of several minutes on a forest road practically flat at a constant speed of 3.3 m/s. The estimated speed then similar to the instant speed, which was also coherent.
We can also analyze the intervals, presented in the following table.
| Circuits | Travel time | Average pace on the move | Pace on Flat Road | Lap Power |
|---|---|---|---|---|
| 1 | 16:57 | 6:04 | 5:58 | 176 |
| 2 | 6:31 | 6:49 | 6:19 | 158 |
| 3 | 6:54.5 | 6:18 | 6:19 | 166 |
| 4 | 14:25 | 4:58 | 4:57 | 210 |
The first interval is used for the learning, the algorithm had no stored data, we can forget it.
The second is on steep path. The only thing you can to conclude is that the pace (6:49) is lower (6:19) than what it would have been on a flat track. But it is impossible to make a statement of the precision of this value.
The third interval corresponds to the soft descent followed by a soft ascent. The pace on a flat track is identical to the measured pace because the value during the rise, stronger, is compensated by the lower value during the descent.
The last interval is the run on the flat road at constant pace of 5:00. Here, the real pace and the pace on a flat track are identical.
Trail test
Why a trail?
After two hours of racing on plains, I decided to test the algorithm on the mountain. This environment has a specific difficulty: there is a risk of disturbance of the algorithm. Indeed, it is not adapted to calibrate due to the lack of flat areas and there is the risk that the algorithm will unlearn the previously learned configuration.
In a caricatured way, by running continuously up and then down, the speed when ascending is much slower than that when descending. Exactly the opposite of the power which is more in correlation of the effort. The result could be that the algorithm assimilates the highs powers to low speeds, which would be nonsense.
The course
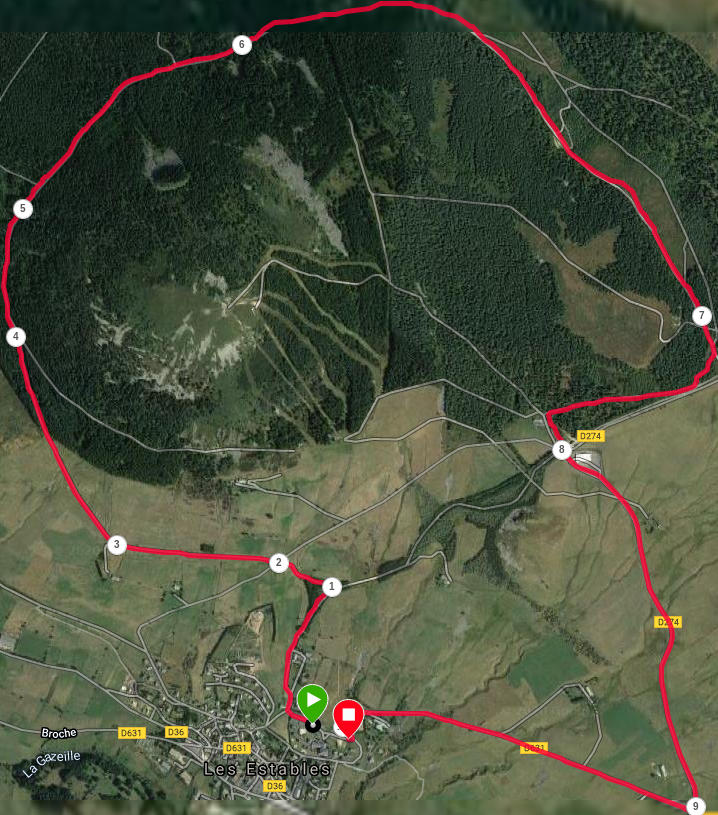
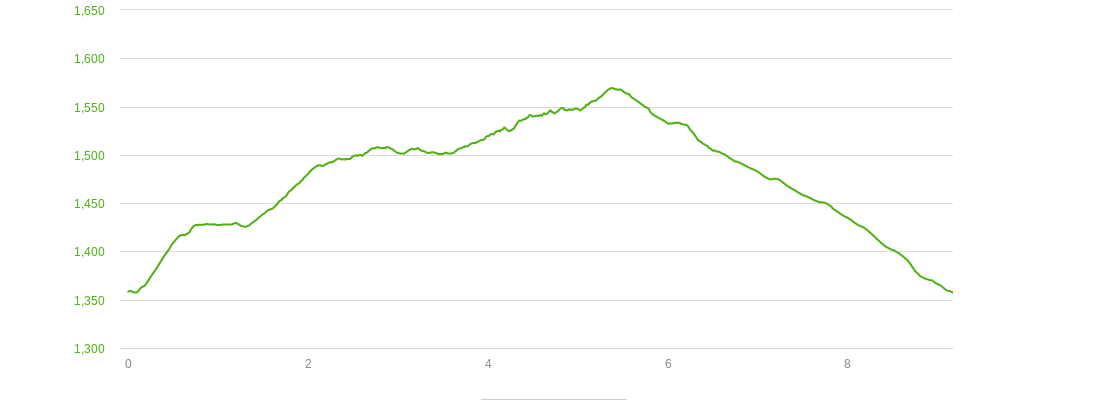
The chosen route is the circuit around the Alambre mountain which is part of the trail from Mézenc.
During the first 500m, the track follows a ski-lift (lap 1). It’s steep and almost difficult to run at the limit to switch back to walking. Then, a succession of flat stretches and regular climbs that remain pleasant to run (laps 2 to 7). The first 500m of downhill (lap 8) are technical because the path requires a minimum of attention (stony road and potholes). For finish, a long descent on asphalt road (laps 9 and 10).
Analysis on Calibration
The first remarkable point is that in general the pace on a flat track remains consistent. I had done, after the calibration run, only 20km of runs on the plains in ideal conditions. Arrived in the mountains, I ran around 70km and the algorithm continued to deliver measurements that were in accordance with the first races.
More precisely:
- On uphills, the flat speed is noticeably greater than that of the measured speed. (and vice versa on downhils). There is therefore a good recognition of these situations and the algorithm does not unlearn the speeds learned on these tracks.
- As soon as we find ourselves on a flat portion, the two speeds are identical.
So the algorithm remains calibrated correctly and correctly detects flat sections to fine tune it.
Step by Step Analysis.
Here is the lap by lap information:
| Circuits | Distance | Gain alt | Loss of altitude | Average pace on the move | Pace on Flat Road | Lap Power |
|---|---|---|---|---|---|---|
| 1 | 0.56 | 53 | - | 8:23 | 5:09 | 197 |
| 2 | 0.21 | 16 | - | 7:49 | 5:50 | 179 |
| 3 | 0.54 | 1 | - | 6:04 | 5:53 | 178 |
| 4 | 0.78 | 56 | - | 7:22 | 5:14 | 194 |
| 5 | 0.44 | 12 | - | 6:08 | 6:20 | 169 |
| 6 | 0.94 | 15 | 11 | 6:12 | 6:05 | 174 |
| 7 | 2.07 | 69 | 5 | 6:44 | 5:50 | 179 |
| 8 | 0.91 | - | 53 | 6:09 | 7:15 | 154 |
| 9 | 1.35 | - | 65 | 5:58 | 6:20 | 169 |
| 10 | 1.29 | - | 86 | 5:36 | 6:43 | 163 |
| 11 | 0.07 | - | 3 | 6:16 | 7:27 | 149 |
The first lap is particular and difficult to interpret. In fact, the slope is greater than 10% and the terrain is particularly steep. I had to run on tiptoes because my heel could no longer touch the ground. And, the ground irregularities were so important that it was difficult to take advantage of the rebound effect. So, I don’t know if the calculated power value by the Stryd sensor corresponds to reality or if I was exhausted due to the fact that I wa not able to run efficiently. Anyway, my impression was to exert an effort far over my critical power (207w) while the Stryd sensor computes something lower. In short, difficult to make judgment on this segment.
Lap 4 and 7, are regular climbs, the speed on a flat track estimate was quite consistent with the effort felt:
- Lap 4: the slope is quite steep, the effort is intense and corresponds here to the feeling of a race more closer to 5:00 than to 6:00
- Lap 7: the ascent slope is gentle and the effort provided was closer to one of my quiet races (6:00).
For the flat portion (lap 3), the speed on a flat track is bit higher than the measured speed. It’s hard to know Why. It could be caused by the nature of terrain (here a stony track and not an asphalt road), by the wind which was lateral but strong or by the fact that it is not really flat (the difference in height reported by my Forerunner 245 watch is not correct since that it does not have a barometric altimeter). But, the estimated speed on a flat track remains sufficiently close to the measured value to correspond to the feeling.
The descent is particularly interesting because I found myself in 3 completely different situations:
- Lap 8: the descent was on typical terrain for trail running. It is a forest path that requires such concentration that it is difficult to run at full speed. The pace is moderate and the pace on a flat track is equivalent that of a very slow warm-up (close to 7:00).
- Lap 9: this section is a downhill road with a regular slope. But, it was made with a strong headwind. Stryd estimated that the power lost was about 7% (with spikes of 19%). During gusts, I took a look at the speed on flat track, it was sometime the same as the actual speed. I felt that the whole effect of the slope was canceled by the wind. It reflects well the measurement because the pace on the flat track (6:20) is lower than that the measured (5:58) but taking into account the slope (5-6%), the difference should have been greater without wind.
- Lap 10: the route is comparable to that of lap 9. Nevertheless, it is oriented so that the wind was lateral and, therefore, its effect its effect is less important. In this situation the pace difference close to what is expected: the speed on the flat track is estimated at 6:43 while the mearured speed is significantly faster with 5:36.
General impression
The general impression of what the estimation of the pace on the track is good. The only downside concerns the too extreme steep slopes but it is difficult to figure out if we are not at the limit of what Stryd can measure since we are at the limit to the running/walking threshold.
Teachings
First of all, it is not necessary to run for hours to obtain consistent velocity values. Nevertheless, it is necessary absolutely run the first few minutes on a flat road and especially to vary the running speeds so that the algorithm learns the associated power from the complete speed range.
Then, the disturbances caused by terrain are well managed and do not interfere with the calculation. We then end up with a value which corresponds to what is expected: as soon as you are on a flat and windless road, the measured and the speed on flat track are identical. On a hill, the gap between the two metrics corresponds to the effort provided.
To be continued….
The application is not finalized, the algorithm is certainly validated but corrections and practical extensions are still under development. And then, the power in the race allows many other developments but this will be for future applications…
-
The article from “GPS Accuracy of Garmin, Polar, and other Running Watches” is very informative about it. ↩︎
-
See the article “How can I convert my pace based plan to a power plan?”. ↩︎
Sharing is caring!